Homepage of Hannes Nickisch

Hannes Nickisch After doing a PhD at the Max Planck Institute for Biological Cybernetics and a PostDoc at the Max Planck Institue for Intelligent Systems, I'm using machine learning and AI methods for medical image analysis tasks e.g. for cardiovascular1,2 and oncology applications as a Senior Scientist at Philips, Hamburg, Germany.

During my study times at the Technical University Berlin and the Université de Nantes I did internships with Microsoft Research in Cambridge, Siemens Corporate Research in Princeton and Siemens Medical Systems in Erlangen.

My research interests lie in probabilistic machine learning, computer vision and pattern recognition, medical image processing and predictive patient-specific biophysical models based on Gaussian processes and neural networks

My work is listed below, and on GoogleScholar Icon ResearchGate Icon Scopus Icon ORCID iD icon Philips icon Clarivate ICON. In case you wish to collaborate or have questions, please contact me via contact.hannes@nickisch.org or LinkedIn ICON.


Code and Data

gpml

GP The Gaussian Process for Machine Learning toolbox.

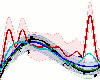gpml A library for Gaussian process regression and classification for Octave/Matlab containing a variety of approximate inference schemes ranging from Laplace's method over expectation propagation to variational Bayes. We furthermore support large scale approximate inference via the FITC approximation and MCMC sampling.
See the mloss.org project (rank #19), the gitlab repository, the JMLR paper and the gpml page. 


    cov = {@covSEiso}; sf = 1; ell = 0.4; hyp.cov = log([ell;sf]);
    lik = 'likLaplace'; sn = 0.2; hyp.lik = log(sn);
    mean = @meanZero;                   % set up GP (cov,lik,mean)
    nlZ = gp(hyp, 'infEP', mean, cov, lik, X, y);      % inference

AwA - Animals with Attributes

CV A dataset for Attribute-Based Classification.

AwA A dataset for benchmarking transfer-learning or zero-shot learning algorithms. The dataset contains 30475 images in 50 animal classes aligned with Osherson's well-known class/attribute matrix with 85 numerical attributes per class.
See the download website, the download website of the free successor dataset, the CVPR paper and the IEEE-TPAMI pdf.


OATH - Oslo Aurora THEMIS dateset

CV A dataset for aurora classification.

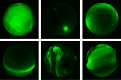OATH A dataset containing manually labeled aurora images from the THEMIS all-sky imagers. The dataset contains a total of 5824 images in 6 different classes "arc", "diffuse", "discrete", "cloudy", "moon" and "clear". It can be used to train classifiers and benchmark algorithms.
See the download website and the NIRD archive for the images and a baseline and the related JGR paper.


glm-ie

ML The Generalised Linear Models Inference and Estimation Toolbox.

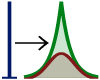glm-ie A library for large scale matrix vector multiplication (MVM) based computations in generalised linear models for Octave/Matlab. We support variational Bayes, factorial mean field and expectation propagation as well as MAP estimation using a wide range of penalised least squares solvers for sparse estimation. A dedicated matrix class provides computational primitives and a wide range of regularisers are supported.
See the mloss.org project (rank #35), the JMLR paper and the glm-ie page. 


    X = matConv2(f, su, 'circ');        % convolution matrix
    B = matFD2(su, 'circ');       % finite difference matrix
    pot = @potLaplace; s2 = 1e-4; tau = 15;
    [m,ga,b,z,nlZ] = dli(X,y,s2,B,pot,tau,opts); % inference
    pen = @(s) penAbs(s);                       % l1-penalty
    [u,phi]  = plsTN(u0,X,y,B,opt,s2,pen);      % estimation

gmm

GP Gaussian mixture modeling with Gaussian process latent variable models and others.

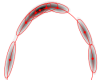dgplvm The toolbox contains code for density estimation using mixtures of Gaussians. Starting from simple kernel density estimation using spherical and diagonal Gaussian kernels over manifold Parzen window until mixtures of penalised full Gaussians with only a few components, the toolbox covers many Gaussian mixture model parametrisation from the recent literature. Most prominently, the package contains code to use the Gaussian process latent variable model for density estimation.
See the mloss.org project and the corresponding DAGM paper or get the code here. 


    [lp,lpte] = dkde(z,zte);      % diagonal kernel density estimation
    [lp,lpte] = mpar(z,zte,d,k);  % manifold Parzen windows
    [lp,lpte] = pgau(z,zte);      % penalised Gaussian

fwtn

The fast wavelet transformation for tensor data.

fwtn The code contains a standalone light-weight implementation of the orthonormal wavelet transform using quadrature mirror filters in C including a Matlab/MEX wrapper. We fully support D-dimensional data in L levels. The algorithm has a computational complexity linear in the size of the input.
See the mloss.org project or get the code here.


    qmf = [1,1]/sqrt(2); % Haar wavelet
    L   = 3;             % # levels in the pyramid
    W   = fwtn(X,L,qmf); % apply FWT, inverse: X = fwtn(W,L,qmf,1);

approxXX

GP A variety of approximate inference methods for Gaussian process prediction.

approxXX The code comprises expectation propagation, Laplace's method, the informative vector machine, Gaussian variational mean field, factorial mean field, on-line expectation propagation, TAP and variational bounding. Note that is numerically much less robust than the code in gpml. The implementations are meant to illustrate the algorithms as such and not for use as a black box system in an applied setting. The functions use the gpml v2.0 Octave/Matlab interface.
See the corresponding JMLR paper or get the code here.


    hyp = [1; 1];       % ell,sig - GP parameters
    cov = {'covSEiso'}; % covariance function
    lik = 'cumGauss';   % logistic or cumGauss likelihood
    apx = 'LA';         % EP,FV,IVM,KL,LA,LR,OLEP,SO,TAP,TAPnaive or VB
    p = binaryGP(hyp, ['approx',apx], cov, lik, x, y, xt); % prediction

Recent Work

Med NN On TotalSegmentator’s performance on low-dose CT images [pdf] [slides] [link]
A. Tsanda, H. Nickisch, T. Wissel, T. Klinder, T. Knopp, M. Grass, SPIE (oral), 2024, accepted.

NN Localized Magnetic Substorm Forecasting using Machine Learning [draft]
P. Sado, L. Clausen, W. Miloch, H. Nickisch, submitted, 2023.

NN Substorm Onset Prediction using Machine Learning Classified Auroral Images [preprint] [link] [code]
P. Sado, L. Clausen, W. Miloch, H. Nickisch, Journal of Geophysical Research - Space Weather, 2023.

Med NN Pulmonary Embolus Detection with Dual-Energy CT Data Augmentation [pdf] [slides] [poster]
C. Hofsäß, R. Gertz, T. Lossau, J. Zemke, T. Knopp, T. Klinder, A. Bunck, H. Nickisch, MIDL short paper (oral), 2022.


Scientific Papers

Journal Articles

23) NN Substorm Onset Prediction using Machine Learning Classified Auroral Images [preprint] [link] [code]
P. Sado, L. Clausen, W. Miloch, H. Nickisch, Journal of Geophysical Research - Space Weather, 2023.

22) Med NN Cascaded learning in intravascular ultrasound: coronary stent delineation in manual pullbacks [pdf] [link]
T. Wissel, K. Riedl, K. Schaefers, H. Nickisch, F. Brunner, N. Schnellbächer, S. Blankenberg, M. Seiffert, M. Grass, Journal of Medical Imaging, 2022.

21) NN Transfer Learning Aurora Image Classification and Magnetic Disturbance Evaluation [preprint] [link] [code]
P. Sado, L. Clausen, W. Miloch, H. Nickisch, Journal of Geophysical Research - Space Physics, 2021.

20) Med NN Smart Chest X-ray Worklist Prioritization using Artificial Intelligence: A Clinical Workflow Simulation [pdf] [pdf] [link]
I. Baltruschat, L. Steinmeister, H. Nickisch, A. Saalbach, M. Grass, G. Adam, T. Knopp, H. Ittrich, European Radiology, 2020.

19) Med NN Learning Metal Artifact Reduction in Cardiac CT Images with Moving Pacemakers Medical Image Analysis [pdf] [link]
T. Lossau (Elss), H. Nickisch, T. Wissel, M. Morlock, M. Grass, Medical Image Analysis, 61:101655, 2020.

18) Med NN Motion Estimation and Correction in Cardiac CT Angiography Images using Convolutional Neural Networks [pdf] [link]
T. Lossau (Elss), H. Nickisch, T. Wissel, R. Bippus, H. Schmitt, M. Morlock, M. Grass, Computerized Medical Imaging and Graphics, 76:101640, 2019.

17) GP Change Surfaces for Expressive Multidimensional Changepoints and Counterfactual Prediction [pdf] [link]
W. Herlands, D. B. Neill, H. Nickisch, A. G. Wilson, Journal of Machine Learning Research, 20(99):1−51, 2019.

16) Med NN Comparison of Deep Learning Approaches for Multi-Label Chest X-Ray Classification [pdf] [link]
I. Baltruschat, H. Nickisch, M. Grass, T. Knopp, A. Saalbach, NSR, 9:6381, 2019.

15) Med NN Motion Artifact Recognition and Quantification in Coronary CT Angiography using Convolutional Neural Networks [pdf] [link]
T. Lossau (Elss), H. Nickisch, T. Wissel, R. Bippus, M. Morlock, M. Grass, Medical Image Analysis, 52:68-79, 2019.

14) NN Automatic classifcation of auroral images from the Oslo Auroral THEMIS (OATH) dataset using machine learning [pdf] [link]
[data]
L. Clausen, H. Nickisch, Journal of Geophysical Research - Space Physics, 123(7):5640-5647, 2018.

13) Med A Functionally Personalized Boundary Condition Model to Improve estimates of fractional flow reserve with CT (CT-FFR) [pdf] [link]
M. Freiman, H. Nickisch, H. Schmitt, P. Maurovich-Horvat, P. Donnelly, M. Vembar and L. Goshen, Medical Physics, 45(3):1170-1177, 2018.

12) Med Improving CCTA based lesions’ hemodynamic significance assessment by accounting for partial volume modeling in automatic coronary lumen segmentation [pdf]
M. Freiman, H. Nickisch, S. Prevrhal, H. Schmitt, M. Vembar, P. Maurovich-Horvat, P. Donnelly and L. Goshen, Medical Physics, 44(3):1040-1049, 2017.

11) Med Blind Multi-Rigid Retrospective Motion Correction of MR Images [pdf] [link]
A. Loktyushin, H. Nickisch, R. Pohmann and B. Schölkopf, Magnetic Resonance in Medicine, 73(4):1457-1468, 2015.

10) CV Attribute-Based Classification for Zero Shot Visual Object Categorization [pdf] [link]
C. Lampert, H. Nickisch and S. Harmeling, IEEE Transactions on Pattern Analysis and Machine Intelligence, 36(3):453-465, 2014.

9) Med Bio Generating Anatomical Models of the Heart and the Aorta from Medical Images for Personalized Physiological Simulations [pdf] [link]
J. Weese, A. Groth, H. Nickisch, H. Barschdorf, F.M. Weber, J. Velut, M. Castro, C. Toumoulin, J.L. Coatrieux, M. De Craene, G. Piella, C. Tobón-Gomez, A.F. Frangi, D.C. Barber, I. Valverde, Y. Shi, C. Staicu, A. Brown, P. Beerbaum and D.R. Hose, Medical and Biological Engineering and Computing, 51(11):1209-1219, 2013.

8) Med Blind Retrospective Motion Correction of MR Images [pdf] [link]
A. Loktyushin, H. Nickisch, R. Pohmann and B. Schölkopf, Magnetic Resonance in Medicine, 70(6):1608-1618, 2013.

7) CV User-centric Learning and Evaluation of Interactive Segmentation Systems [pdf] [link]
P. Kohli, H. Nickisch, C. Rother and C. Rhemann, International Journal of Computer Vision, 100(3):261-274, 2012.

6) ML Generating Feature Spaces for Linear Algorithms with Regularized Sparse Kernel Slow Feature Analysis [pdf] [link]
W. Böhmer, S. Grünewälder, H. Nickisch, K. Obermayer, Machine Learning, 89(1):67-86, 2012.

5) ML glm-ie: The Generalised Linear Models Inference and Estimation Toolbox [pdf] [web] [link]
H. Nickisch, Journal of Machine Learning Research, 13:1699-1703, 2012.

4) ML Large Scale Bayesian Inference and Experimental Design for Sparse Linear Models [pdf] [link]
M. W. Seeger and H. Nickisch, SIAM Journal on Imaging Sciences, 4(1):166-199, 2011.

3) GP Gaussian Processes for Machine Learning (GPML) Toolbox [pdf] [web] [link]
C. E. Rasmussen and H. Nickisch, Journal of Machine Learning Research, 11:3011-3015, 2010.

2) Med Optimization of k-Space Trajectories for Compressed Sensing by Bayesian Experimental Design [pdf] [link]
M. W. Seeger, H. Nickisch, R. Pohmann and B. Schölkopf, Magnetic Resonance in Medicine, 63(1):116-126, 2010.

1) GP Approximations for Binary Gaussian Process Classification [pdf] [link]
H. Nickisch and C. E. Rasmussen, Journal of Machine Learning Research, 9:2035-2078, 2008.

 

Peer-Reviewed Conference Papers

31) Med NN On TotalSegmentator’s performance on low-dose CT images [pdf] [slides] [link]
A. Tsanda, H. Nickisch, T. Wissel, T. Klinder, T. Knopp, M. Grass, SPIE (oral), 2024, accepted.

30) Med NN Pulmonary Embolus Detection with Dual-Energy CT Data Augmentation [pdf] [slides] [poster]
C. Hofsäß, R. Gertz, T. Lossau, J. Zemke, T. Knopp, T. Klinder, A. Bunck, H. Nickisch, MIDL short paper (oral), 2022.

29) Med NN Multi-Resolution 3D convolutional neural networks for automatic coronary centerline extraction in cardiac CT angiography scans [pdf] [pdf] [slides]
Z. Salahuddin, M. Lenga, H. Nickisch, ISBI (oral), 2021.

28) Med NN Machine-learning based clinical plaque detection using a synthetic plaque lesion model for coronary CTA [pdf] [poster] [slides] [link]
N. Schnellbächer, H. Ragab, H. Nickisch, T. Wissel, C. Spink, G. Lund, M. Grass, SPIE, 2021.

27) Med NN Delineation of coronary stents in intravascular ultrasound pullbacks [pdf] [link]
T. Wissel, K. Riedl, K. Schaefers, H. Nickisch, F. Brunner, N. Schnellbächer, S. Blankenberg, M. Seiffert, M. Grass, SPIE (oral), 2021.

26) Med NN How to learn from unlabeled volume data: Self-Supervised 3D Context Feature Learning [pdf] [link] [code]
M. Blendowski, H. Nickisch, M. Heinrich, MICCAI, 2019.

25) Med NN Dynamic Pacemaker Artifact Removal (DyPAR) from CT Data using CNNs [pdf] [link]
T. Lossau, H. Nickisch, T. Wissel, S. Hakmi, C. Spink, M. Morlock, M. Grass, MIDL (oral), 2019.

24) Med NN When does Bone Suppression and Lung Field Segmentation Improve Chest X-Ray Disease Classification? [link]
I. Baltruschat, L. Steinmeister, H. Ittrich, G. Adam, H. Nickisch, A. Saalbach, J. von Berg, M. Grass, T. Knopp, ISBI, 2019.

23) GP State Space Gaussian Processes with Non-Gaussian Likelihood [pdf] [poster] [slides] [link]
H. Nickisch, A. Solin, A. Grigorievskiy, ICML, 2018.

22) Med NN 2D Motion Estimation in Coronary CT Angiography Images using Convolutional Neural Networks [pdf] [poster] [link]
T. Elss, H. Nickisch, T. Wissel, R. Bippus, M. Morlock, M. Grass, MIDL, 2018.

21) Med NN Deep-Learning-Based CT Motion Artifact Recognition in Coronary Arteries [pdf] [slides] [link]
T. Elss, H. Nickisch, T. Wissel, H. Schmitt, M. Vembar, M. Morlock, M. Grass, SPIE (oral), 2018.

20) Med NN Orientation Regression in Hand Radiographs: A Transfer Learning Approach [pdf] [link]
I. Baltruschat, A. Saalbach, M. Heinrich, H. Nickisch, S. Jockel, SPIE (poster award), 2018.

19) Med Nearest Neighbor 3D Segmentation with Context Features [pdf] [slides] [link]
E. Hristova, H. Schulz, T. Brosch, M. Heinrich, H. Nickisch, SPIE (oral), 2018.

18) GP Scalable Log Determinants for Gaussian Process Kernel Learning [pdf] [poster] [code] [link]
K. Dong, D. Eriksson, H. Nickisch, D. Bindel, A. G. Wilson, NIPS, 2017.

17) Med Learning a sparse database for patch-based medical image segmentation [pdf]
M. Freiman, H. Nickisch, H. Schmitt, P. Maurovich-Horvat, P. Donnelly, M. Vembar, L. Goshen, MICCAI PatchMI, 2017.

16) GP Scalable Gaussian Processes for Characterizing Multidimensional Change Surfaces [pdf] [poster] [slides] [link]
W. Herlands, A. G. Wilson, H. Nickisch, S. Flaxman, D. B. Neill, W. van Panhuis, E. Xing, AISTATS, 2016.

15) Med Automatic coronary lumen segmentation with partial volume modeling improves hemodynamic significance assessment [pdf] [slides] [link]
M. Freiman, Y. Lamash, G. Gilboa, H. Nickisch, S. Prevrhal, H. Schmitt, M. Vembar and L. Goshen, SPIE (oral), 2016.

14) Med ML SVM-based failure detection of GHT localizations [pdf] [slides] [link]
T. Blaffert, C. Lorenz, H. Nickisch, J. Peters and J. Weese, SPIE (oral), 2016.

13) Med Bio Learning Patient-Specific Lumped Models for Interactive Coronary Blood Flow Simulations [pdf] [talk] [slides]
H. Nickisch, Y. Lamash, S. Prevrhal, M. Freiman, M. Vembar, L. Goshen and H. Schmitt, MICCAI (oral), 2015.

12) GP Kernel Interpolation for Scalable Structured Gaussian Processes (KISS-GP) [pdf, [supp] [slides] [link]
A. G. Wilson and H. Nickisch, ICML, 2015.

11) GP Fast Kronecker Inference in Gaussian Processes with non-Gaussian Likelihoods [pdf] [link]
S. Flaxman, A. G. Wilson, D. B. Neill, H. Nickisch, and A. Smola, ICML, 2015.

10) Med From Image to Personalized Cardiac Simulation: Encoding Anatomical Structures into a Model-Based Segmentation Framework [pdf] [link] [poster]
H. Nickisch, H. Barschdorf, F. M. Weber, M. W. Krueger, O. Dössel and J. Weese, MICCAI STACOM, 2012.

9) GP Additive Gaussian Processes [pdf] [link]
D. Duvenaud, H. Nickisch and C. E. Rasmussen, NIPS, 2011.

8) ML Regularized Sparse Kernel Slow Feature Analysis [pdf] [link]
W. Böhmer and S. Grünewälder, H. Nickisch and K. Obermayer, ECML/PKDD, 2011.

7) ML Fast Convergent Algorithms for Expectation Propagation Approximate Bayesian Inference [pdf] [link]
M. W. Seeger and H. Nickisch, AISTATS, 2011.

6) CV Learning an interactive segmentation system [pdf] [link]
H. Nickisch, C. Rother, C. Rhemann and Pushmeet Kohli, ICVGIP, 2010.
Best paper award.

5) GP Gaussian Mixture Modeling with Gaussian Process Latent Variable Models [pdf] [link]
H. Nickisch and C. E. Rasmussen, DAGM, 2010.

4) ML Convex variational Bayesian inference for large scale generalized linear models [pdf] [link]
H. Nickisch and M. W. Seeger, ICML, 2009.

3) CV Learning To Detect Unseen Object Classes by Between-Class Attribute Transfer [pdf] [link]
C. H. Lampert, H. Nickisch and S. Harmeling, CVPR, 2009.

2) Med Bayesian Experimental Design of Magnetic Resonance Imaging Sequences [pdf] [link]
M. W. Seeger, H. Nickisch, R. Pohmann and B. Schölkopf, NIPS, 2008.

1) ML Compressed Sensing and Bayesian Experimental Design [pdf] [link]
M. W. Seeger and H. Nickisch, ICML, 2008.

 

Abstracts and Posters

9) Med NN Effect of Inter-Observer Variability on Deep Learning in Chest X-Rays
M. Grass, I. M. Baltruschat, A. Saalbach, H. Nickisch, J. von Berg, G. Adam, L. Steinmeister, H. Ittrich, T. Knopp, ECR, C-1093, 2019.

8) Med NN Effect of Advanced Image Pre-Processing for Multi-Label Chest X-Ray Classification
H. Ittrich, I. M. Baltruschat, L. A. Steinmeister, M. Grass, A. Saalbach, T. Knopp, G. Adam, H. Nickisch, RSNA, AI200-SD-SUA1, 2018.

7) Med NN Comparison of deep learning-based techniques for organ segmentation in abdominal CT images [pdf] [link]
V. Groza, T. Brosch, D. Eschweiler, H. Schulz, S. Renisch, H. Nickisch, MIDL, 2018.

6) GP Med Dual Compartment Regression for the Generation of Pseudo-CT Images [pdf] [link]
A. Schnurr, E. Orasanu, H. Schulz, H. Nickisch, S. Renisch, AAPM, SU-K-601, 2017.

5) Med Improved On-Site FFR-CT Accuracy by Coronary Tree Standardization [link, p.362]
H. Nickisch, M. Freiman, S. Prevrhal, M. Vembar, P. Donnelly, P. Maurovich-Horvat, L. Goshen, H. Schmitt, ECR, SS 1003, 2017.

4) GP Is Gun Violence Contagious? Descriptive Spatio-Temporal Testing and Modeling with Large-Scale Point Process [link]
C. Loeffler, S Flaxman, W. Herlands, H. Nickisch, JSM (Methods for Massive Spatial Data, Statistics and the Environment), 2016.

3) Med NN Can Pretrained Neural Networks Detect Anatomy? [link]
V. Menkovski, Z. Aleksovski, A. Saalbach, H. Nickisch, NIPS Workshop on Machine Learning in Healthcare, 2015.

2) Med FID-guided retrospective motion correction based on autofocusing
M. Babayeva, A. Loktyushin, T. Kober, C. Granziera, H. Nickisch, R. Gruetter, G. Krueger, ISMRM-ESMRMB, 2014.

1) ML Experimental design for genome-wide association studies [pdf]
C. Lippert, O. Stegle, H. Nickisch, K. Borgwardt, D. Weigel, ISMB, 2010.

 

Diploma and PhD Theses

2) GP ML Bayesian Inference and Experimental Design for Large Generalised Linear Models [pdf] [link]
H. Nickisch, PhD Thesis, Technische Universität Berlin, Berlin, Germany, 2010.

1) ML Extraction of visual features from natural video data using Slow Feature Analysis [pdf]
H. Nickisch, Diploma Thesis, Technische Universität Berlin, Berlin, Germany, 2006.

 

Technical Reports

See arXiv.org for a list of more technical reports.

2) GP Thoughts on Massively Scalable Gaussian Processes [link]
A. G. Wilson, C. Dann and H. Nickisch, arXiv.org, 2015.

1) GP Multiple Kernel Learning: A Unifying Probabilistic Viewpoint [pdf] [link]
H. Nickisch and M. W. Seeger, arXiv.org, 2011.


Intellectual Property

See USPTO (Nickisch AND Philips) or Justia for the list of my granted US patents and applications (18 grants and 31 applications as of January 2024).

Granted US Patents

18) Resolving and steering decision foci in machine learning-based vascular imaging US11721439B2, 2023-08-08

17) Standardized coronary artery disease metric US11576637B2, 2023-02-14

16) Interaction monitoring of non-invasive imaging based FFR US11523744B2, 2022-12-13

15) Fractional flow reserve determination US11490867B2, 2022-11-08

14) Coronary artery health state prediction based on a model and imaging data US11301994B2, 2022-04-12

13) Fractional flow reserve simulation parameter customization, calibration and/or training US11195278B2, 2021-12-07

12) Apparatus for determining a functional index for stenosis assessment US11179043B2, 2021-11-23

11) Fractional flow reserve determination US11141123B2, 2021-10-12

10) Vascular tree standardization for biophysical simulation and/or an extension simulation for pruned portions US11055845B2, 2021-07-06

9) Apparatus and method for determining a fractional flow reserve US11039804B2, 2021-06-22

8) Mobile FFR simulation US10898267B2, 2021-01-26

7) Heart model guided coronary artery segmentation US10902606B2, 2021-01-26

6) Model-based segmentation of an anatomical structure US10282846B2, 2019-05-07

5) Apparatus for determining a fractional flow reserve value US10258303B2, 2019-04-16

4) Local FFR estimation and visualisation for improved functional stenosis analysis US10111633B2, 2018-10-30

3) Method of determining the blood flow through coronary arteries US9867584B2, 2018-01-16

2) Segmentation apparatus for interactively segmenting blood vessels in angiographic image data US9842401B2, 2017-12-12

1) Processing apparatus for processing cardiac data US9788807B2, 2017-10-17

US Patent Applications

31) METHOD AND SYSTEM FOR VISUALIZATION US20230410307A1, 2023-12-21

30) MEDICAL IMAGE POST-PROCESSING US20230386644A1, 2023-11-30

29) FOCUS OPTIMIZATION FOR PREDICTION IN MULTI-FREQUENCY ULTRASOUND IMAGING US20230148382A1, 2023-05-11

28) UNCERTAINTY-BASED REPRIORITIZATION OF MEDICAL IMAGES BASE UPON CRITICAL FINDINGS US20230077721A1, 2023-03-16

27) CORONARY ARTERY DISEASE METRIC BASED ON ESTIMATION OF MYOCARDIAL MICROVASCULAR RESISTANCE FROM ECG SIGNAL US20210118569A1, 2021-04-22

26) FRACTIONAL FLOW RESERVE SIMULATION PARAMETER CUSTOMIZATION, CALIBRATION AND/OR TRAINING US20210110543A1, 2021-04-15

25) METHOD AND APPARATUS FOR PHYSIOLOGICAL FUNCTIONAL PARAMETER DETERMINATION US20210100522A1, 2021-04-08

24) SIMULATION OF TRANSCATHETER AORTIC VALVE IMPLANTATION (TAVI) INDUCED EFFECTS ON CORONARY FLOW AND PRESSURE US20210093382A1, 2021-04-01

23) CORONARY ARTERY HEALTH STATE PREDICTION BASED ON A MODEL AND IMAGING DATA US20210073978A1, 2021-03-11

22) SYSTEM AND METHOD FOR IMAGE DECOMPOSITION OF A PROJECTION IMAGE US20200410673A1, 2020-12-31

21) RESOLVING AND STEERING DECISION FOCI IN MACHINE LEARNING-BASED VASCULAR IMAGING US20200411189A1, 2020-12-31

20) INTERACTIVE SELF-IMPROVING ANNOTATION SYSTEM FOR HIGH-RISK PLAQUE BURDEN ASSESSMENT US20200402646A1, 2020-12-24

19) INTRAVASCULAR NAVIGATION USING DATA-DRIVEN ORIENTATION MAPS US20200397294A1, 2020-12-24

18) FRACTIONAL FLOW RESERVE DETERMINATION US20200337664A1, 2020-10-29

17) INFLAMMATION ESTIMATION FROM X-RAY IMAGE DATA US20200226749A1, 2020-07-16

16) STANDARDIZED CORONARY ARTERY DISEASE METRIC US20200060637A1, 2020-02-27

15) INTERACTION MONITORING OF NON-INVASIVE IMAGING BASED FFR US20200037893A1, 2020-02-06

14) SPECTRAL IMAGING FFR US20200034968A1, 2020-01-30

13) VASCULAR TREE STANDARDIZATION FOR BIOPHYSICAL SIMULATION AND/OR AN EXTENSION SIMULATION FOR PRUNED PORTIONS US20190318475A1, 2019-10-17

12) APPARATUS AND METHOD FOR DETERMINING A FRACTIONAL FLOW RESERVE US20190209115A1, 2019-07-11

11) FRACTIONAL FLOW RESERVE DETERMINATION US20190083052A1, 2019-03-21

10) MOBILE FFR SIMULATION US20190038356A1, 2019-02-07

9) CT PERFUSION PROTOCOL TARGETING US20180360405A1, 2018-12-20

8) HEART MODEL GUIDED CORONARY ARTERY SEGMENTATION US20180365838A1, 2018-12-20

7) PROCESSING APPARATUS AND METHOD FOR PROCESSING CARDIAC DATA OF A LIVING BEING US20170245824A1, 2017-08-31

6) APPARATUS FOR DETERMINING A FRACTIONAL FLOW RESERVE VALUE US20170105694A1, 2017-04-20

5) MODEL-BASED SEGMENTATION OF AN ANATOMICAL STRUCTURE US20160379372A1, 2016-12-29

4) LOCAL FFR ESTIMATION AND VISUALISATION FOR IMPROVED FUNCTIONAL STENOSIS ANALYSIS US20160302750A1, 2016-10-20

3) PROCESSING APPARATUS FOR PROCESSING CARDIAC DATA US20160206265A1, 2016-07-21

2) SEGMENTATION APPARATUS FOR INTERACTIVELY SEGMENTING BLOOD VESSELS IN ANGIOGRAPHIC IMAGE DATA US20160196660A1, 2016-07-07

1) METHOD OF DETERMINING THE BLOOD FLOW THROUGH CORONARY ARTERIES US20150297161A1, 2015-10-22


Student Supervision and Reviewing

Students (co-)supervised

13) Med NN Machine Learning in Auroral Image Research; Aurora Image Classification using Machine Learning Techniques and Substorm Forecasting [disputation] [pdf]
Pascal Sado, PhD Thesis, University of Oslo, Oslo, Norway, 2023.

12) Med NN Generalizability of Deep-Learning-Based Pulmonary Embolism Detection from CT Data [pdf]
Cornelia Hofsäß, Master Thesis, Hamburg University of Technology, Hamburg, Germany, 2022.

11) Med NN Exploiting Long-Range Dependencies for Prediction of Biomarkers in Coronary Artery Disease
Danil Zamnius, Master Thesis, Universität zu Lübeck, Lübeck, Germany, 2022.

10) Med NN Deep Learning for Automatic Lung Disease Analysis in Chest X-rays [pdf]
Ivo Baltruschat, PhD Thesis, Hamburg University of Technology, Hamburg, Germany, 2021.

9) Med NN Efficient Object Detection in 3D CT Scans [pdf]
Jannis van Kersbergen, Master Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2021.

8) Med NN Multi-Resolution 3D Convolutional Neural Networks for Automatic Coronary Centerline Extraction in Cardiac CT Angiography Scans [link] [preprint] [pdf]
Zohaib Salahuddin, Master Thesis, MAIA Erasmus Mundus, Dijon/Cassino/Girona, France/Italy/Spain (best student award), 2020.

7) Med NN Machine Learning in Cardiac CT Image Reconstruction [book] [pdf]
Tanja Lossau, PhD Thesis, Hamburg University of Technology, Hamburg, Germany, 2020.

6) Med NN Sparse Convolutional Neural Networks in 3D Medical Image Segmentation
Yuan Yao, Master Thesis, Technical University of Berlin, Berlin, Germany, 2019.

5) Med NN A Tool for Visualizing, Analyzing and Debugging Neural Networks
Laurin Mordhorst, Master Thesis, Hamburg University of Technology, Hamburg, Germany, 2018.

4) Med ML 3D Medical Image Segmentation with Vantage Point Forests and Binary Context Features [pdf]
Evelin Hristova, Master Thesis, Hamburg University of Applied Sciences, Hamburg, Germany, 2017.

3) Med NN Deep Learning for Advanced Medical Applications
Ivo Baltruschat, Master Thesis, Universität zu Lübeck, Lübeck, Germany, 2016.

2) Med Blind Retrospective Motion Correction of MR Images [link] [pdf] [pdf]
Alexander Loktyushin, PhD Thesis, University of Tübingen, Tübingen, Germany, 2015.

1) Med Model Generation for Automatic Myocardium Segmentation.
Jan Wingerter, Diploma Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2013.

Reviewing

See Clarivate ICON Web of science and ORCID iD icon ORCID for a summary.

Machine Learning Conferences
NIPS/NeurIPS (2009-2011, 2013-2023), ICML (2009, 2011, 2016-2024), ICLR (2019-2024), AAAI (2018, 2020), AISTATS (2009-2012), COLT (2010), DAGM/GCPR (2009)
(Medical) Image Processing Conferences
MICCAI (2013, 2018-2024), MIDL (2019-2020), ICCV (2009)
Machine Learning Journals
JMLR, Neurocomputing, IEEE-TPAMI, IEEE-TNNLS, Machine Learning
(Medical) Image Processing Journals
SIIMS, AIIM, Medical Image Analysis, IEEE-TMI, IEEE-TIP, IEEE-TBME, IET-IP, PMB, MVAP, MBEC
Other(s)
Nature Communications, IEEE-TII, IEEE-TETC, IEEE-TMRB, Physiological Measurement, CMBBE, JoVE, AGU, JGR Space Physics, Earth and Space Science

© 2011-2024 Hannes Nickisch

XHTML | CSS | Design by FullAhead